前言
筆者在GAMES 101的Homework 5,遇到Screen Space -> World Space的問題,所以將思路及其解決方法記錄在此篇文章中。在作業5中,有兩題:
- 判斷是否與三角形相交 (Moller-Trumbore)
- 得到射線的方向
此篇文章只說明第2題。
推導
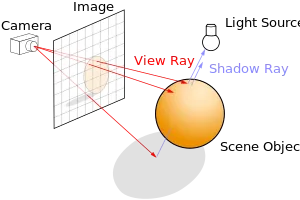
首先,已知Camera的世界座標。並根據代碼,得知投影平面位於Camera的z=-1的位置。
1
| Vector3f dir = Vector3f (x, y, -1);
|
為了得到射線,需要知道Camera與像素中心之間的方向。所以需要計算像素的世界座標,目前已知z=-1,還需要求出x與y。
假設屏幕大小為width×height,起點在左下角,寬高比A=heightwidth。按照以下的步驟進行計算:
-
變換到NDC空間中,NDC空間的範圍為[0,1]
Xndc=widthXscreen+0.5Yndc=heightYscreen+0.5
-
起點變換至中心
X=2×Xndc−1Y=2×Yndc−1
-
根據寬高比拉伸
X=X×AY=Y
一般規定了高為2,所以Y不需要改變。
-
FOV控制視野範圍
一般FOV有水平和垂直之分,作業中的FOV只有一種,即說明水平和垂直的FOV都一樣。
在透視投影中說明的將點投影到近平面上的算式將其逆轉過來,得
Xfinal=X×tan(2fovx)Yfinal=Y×tan(2fovy)
重溫透視投影的算式(右手座標系)
x′=−zxd=−ztan2θxy′=−zyd=−ztan2θy
結論
整理式子,得:
Xfinal=2×(widthXscreen+0.5−1)×A×tan(2fovx)Yfinal=2×(heightYscreen+0.5−1)×tan(2fovy)
改變觀察方向
因為作業中的觀察方向是(0, 0, -1),那麼如何旋轉視角?其實很簡單,只需要將求得的dir乘以旋轉矩陣便可。
1
2
3
4
|
Vector3f dir = Vector3f (x, y, -1);
float angle = 45;
Vector3f new_dir = get_x_rotation_matrix (angle) * dir;
|
相當於將Camera(投影平面)旋轉了45度角。
References
Ray-Tracing: Generating Camera Rays
GAMES 101: 作業5解析